Home > AI Solutions > Artificial Intelligence > White Papers > Memory Consumption Modeling of Deep Learning Workloads > Pandora – symbolic regression based modeling tool
Pandora – symbolic regression based modeling tool
-
The Pandora tool [8] was developed initially for the purposing of approximate computing – to provide inexpensive solutions for complex computing tasks within a reasonable amount of error tolerance. By combing through various mathematical possibilities to arrive at the same solution through empirical modeling, the tool can be used for many regression/curve-fitting tasks. Previous work involved using Pandora for compiler optimization – exploring different approximations for sequential code containing loop carried dependencies [8].
In addition to approximation computing, Pandora has been customized for application and architecture performance modelling [4]. In particular, Pandora provides the three desirable characteristics that are crucial for performance modeling of large-scale systems:
- domain-agnostic
- true multi-parameter modeling
- feasible model generation time
Domain-agnostic is a desirable property so the approach can be applicable to a wider range of applications and systems. Detailed knowledge of the application and target system being modeled is not required. Also, in most cases, the performance of an application or system sub-component to be modeled can have multiple parameters that affect its performance. Hence, the modeling approach should not be restricted to a limited number of parameters to generate an accurate performance model. Finally, the model generation times should be fast enough for iterative refinement if necessary.
In our previous work [4], we performed a systematic study to evaluate the accuracy of the performance models generated using Pandora for various High-Performance Computing (HPC) applications. In that study, it was shown that multi-parameter modeling using symbolic regression (Pandora) was able to generate accurate models with less than 8% MAPE, while using relatively fewer training samples as compared to other machine-learning based regression methods. In this paper, we use Pandora to generate a memory consumption model for 3D U-net application. We validate our model by comparing the predicted results against the measured peak memory performance (test data) of the application. Subsequently, we perform a comparative evaluation of the symbolic regression approach with other prominent ML based regression methods for memory consumption modeling.
Model generation process
In this sub-section, we briefly describe how Pandora generates an analytical model by leveraging symbolic regression principles. While there are multiple strategies to perform symbolic regression, Pandora makes use of genetic programming [5,10,11], not to be confused with more general genetic algorithms. Genetic programming imitates the processes of evolution to develop a solution to a problem. For the purposes of symbolic regression, genetic programming defines genes consisting of mathematical primitives. These primitives are generally basic, low-level operations (such as add, multiply, and so on) but can potentially be arbitrarily complex operations. Figure 7 shows the steps involved in the model generation process. Genetic programming initially creates a population of individuals, which for symbolic regression consists of random equations built from the defined primitives. Genetic programming then evolves different solutions over a number of generations, where each generation involves crossover/reproduction and mutation [5, 12]. Before the end of each generation, a selection process (analogous to natural selection) removes a percentage of individuals from the population based on a pre-defined fitness function. This process generally iterates for either a pre-defined number of generations, or until there is a lack of improvements for a number of generations.
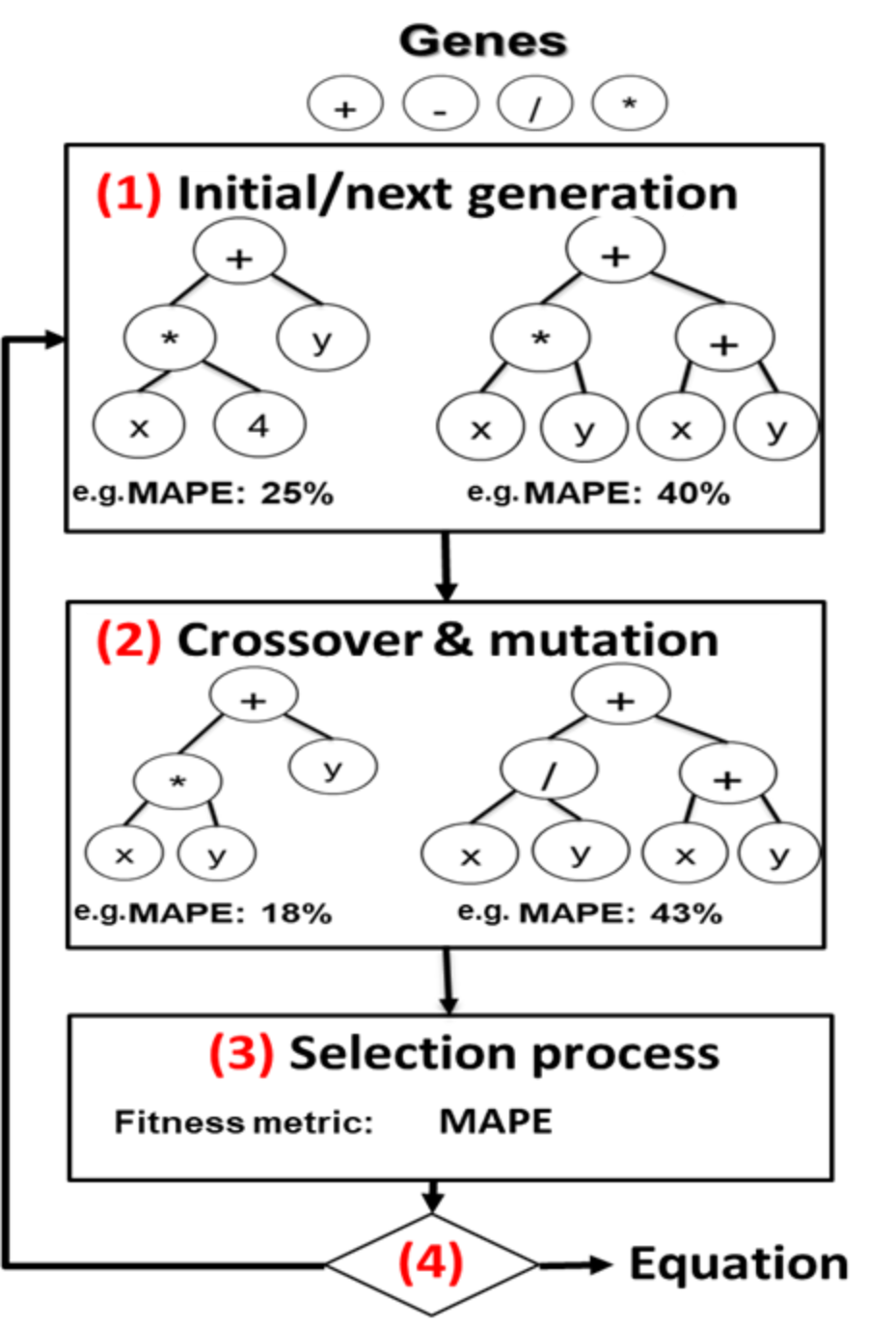
Figure 7. Model generation process in Pandora
Genetic programming is guided by a provided fitness function that specifies desirable characteristics of an individual. For symbolic regression, the most basic fitness function is an error metric. For situations where simple equations are preferable, the function can also include the size, computational complexity, and so on, of the equation. Although any error metric can be used for symbolic regression, common examples include root mean-squared error (RMSE), mean-squared error (MSE), and mean absolute-percentage error (MAPE). Because we are using symbolic regression to generate peak memory consumption models, we will use MAPE, which is useful for showing how closely a set of test/training data fits the regression model.
To perform symbolic regression, we provide Pandora with a configuration file that specifies a number of genetic-programming parameters: training data, test data, primitives/genes, mutation probability, crossover probability, fitness function, population size, and number of generations. Although domain knowledge can be used to fine-tune the configuration file, in our experiments we used the same configuration for all experiments to provide a lower bound on the quality of the results, and to demonstrate that symbolic regression can perform well even without any deep knowledge of the application or architecture being modeled. Our memory consumption model was built using primitives consisting of addition and multiplication. We also included square and cube as primitives, because we expected these to be common in our memory consumption model. Although symbolic regression can generally discover square and cube operations with multiply primitives, inclusion of the square and cube primitive can reduce training times. We have eliminated other basic arithmetic primitives such as subtraction and division because it is not natural for them to be in the memory consumption model.
For all experiments, we used a plus-selection evolutionary algorithm [12], which considers both the parents and offspring during selection. The selection algorithm used a double tournament method [13], with a parsimony size of 1.1 and a fitness size of 3. We used five different mutation operators [9] that the tool selected randomly for each mutation. We used a one-point crossover operator. The mutation probability for each individual was 50%. Crossover probability was 100%. For all examples, we used a population size of 300 with 150 total generations. We empirically determined these values to work well for most symbolic-regression problems we have evaluated. A complete tradeoff exploration of all genetic-programming parameters is outside the scope of this study, but has been studied extensively in evolutionary-algorithm studies [14]. To optimize constants, we used the Levenberg–Marquardt non-linear least squares algorithm [15]. Upon completion, the tool outputs the resulting equation and then tests that equation against the provided test data to determine the resulting generalization error.
